https://arxiv.org/pdf/2102.01010.pdf
这篇论文使用端到端的训练方法,实现了对于DNS和LES,能得到和baseline的8-10倍精细的网格上相同的精度,和40-80x的加速。方法具有长时稳定性,而且可以应用到训练集之外的外力项和Reynold数。
Method
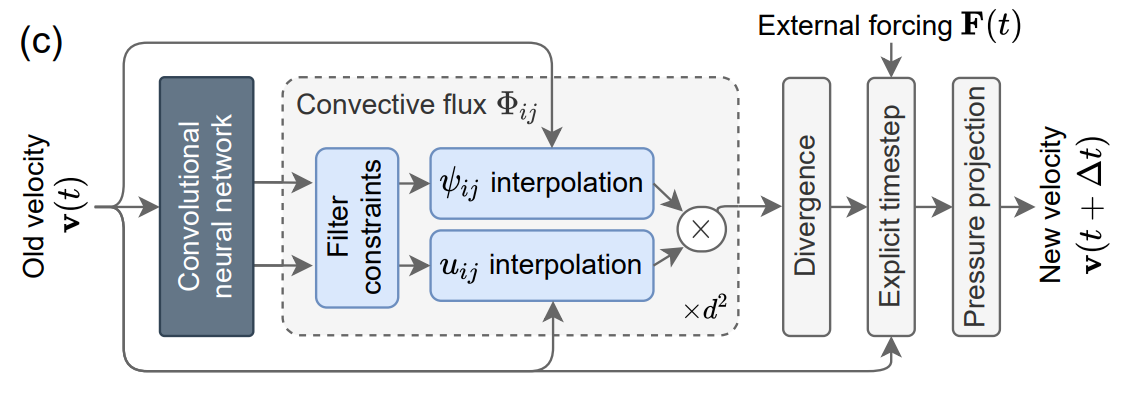
这篇论文首先使用Jax实现了一个可微分的NS求解器(基于有限体积方法,时空一阶的显隐式方法),然后在其中添加了两个可学习的部分:
- 是有限体积方法在重建界面时,一般传统的有constant或者linear到多项式插值,或者WENO等重建方法,这里使用了神经网络来重建边界面的值。其实就是Learning data driven discretizations 中的方法。上图就是这个部分的图解。
- 再用神经网络在每一个时间步后,对解增加一个修正项。
在训练部分,使用了比较寻常的Loss function。在各个时间步累计MSE-Loss。 \[ L(x,y)=\sum_{t_i}^{t_T}MSE(u(t_i),\tilde u(t_i)) \] 训练时将模型展开了32层,这样可以有效提高长时间的稳定性。
训练数据是在高精度的DNS上计算,然后下采样得到的。训练时使用32条不同初值得到的轨迹(每条4800个时间步),然后在更长的轨迹(几万个时间步)上进行测试。有时为了节省显存,使用了checkpoint技术。
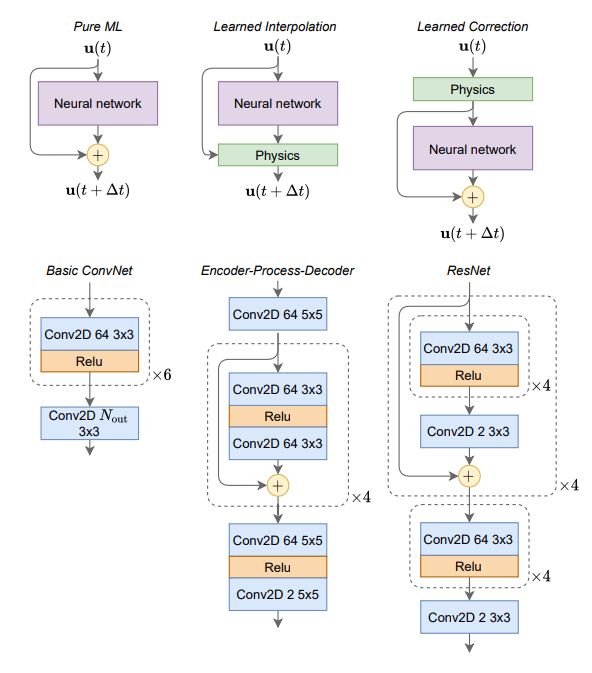
网络结构使用了全卷积神经网络。即下图中的Basic ConvNet。
对于Learned Interpolation, \(N_{out}=120\)。8个量,每个量15个系数。
对于Learned Correction, \(N_{out}=2\)。因为是求解的2D方程,对应速度的两个分量。
数值结果参见:https://mp.weixin.qq.com/s/QmlYIIcG7pjzLfLmFdDnDQ